Amateur mathematician David Smith demonstrated the existence of an einstein, a tile that can be used to tile an entire plane, and the tiling is only non-periodic. According to the preprint of Smith's work, it was co-authored with professional mathematicians Joseph Samuel Myers, Craig Kaplan, and Chaim Goodman-Strauss.
Smith for the first time managed to assemble a parquet from one tile. The figure, which an amateur mathematician came up with, has 13 angles and consists of 16 triangles with angles of 90, 30 and 60 degrees (or eight quadrilaterals, called “kites” for their similarity in shape). The Smith tile is shaped like a hat.
The trick to "assembling" parquet from a "hat" is that the tiles are assembled into "super tiles" of ever larger size. Although no “supertile” is geometrically similar to its constituent tiles, combinatorially the principle of collecting supertiles at each level of increasing complexity does not change.
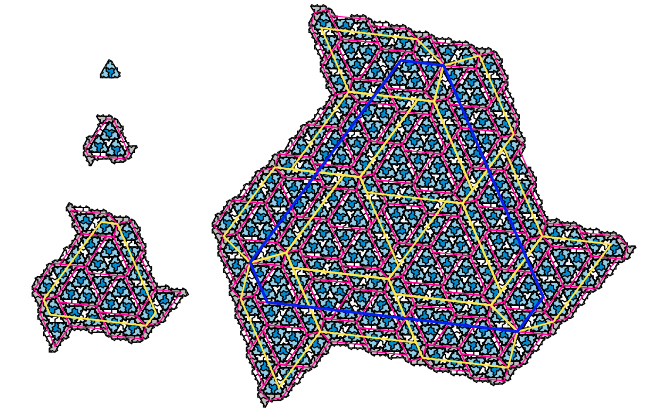
This allows the authors to prove that the process of collecting super-super-tiles from super-tiles, and so on, continues indefinitely, so the “hat” can tile the entire plane, and such tiling will be aperiodic. So the hat is an einstein.
Geometers dealing with tilings of the plane are interested in the Heesch problem. The Heesch number of a figure is the maximum number of "layers" of itself that can surround this figure. So, for a correct tiling of a plane, the Heesch number is equal to infinity. Heesch himself came up with an example of a figure, copies of which can be surrounded by itself only once.
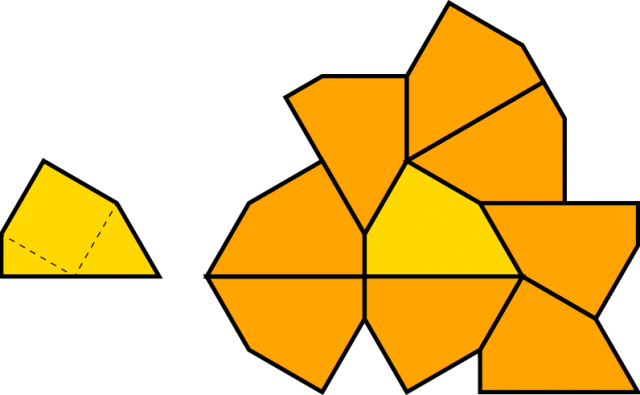
At present, a figure with a maximum finite Heesch number of 6 is known.
Heesch's task is to find out which Heesch numbers exist.
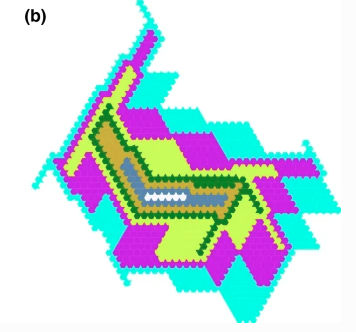
Smith was busy surrounding the hat with replicas of the hat. It might seem that at some point the process will end and it will find a figure with some Heesch number. But the process did not end, and with the help of a program written by Kaplan, it was found that if the hat were not an Einstein, then its Heesch number would be 16. This would already be a fantastic record and a major achievement. And after that it turned out that the hat can pave the entire plane.
The word "einstein", consonant with the name of the famous physicist, comes from the German "ein Stein", which literally means "one stone". More precisely, one tile – like the one that paves the streets. An Einstein is such a tile that the entire plane can be tiled with one tiling, while the tiling can only be non-periodic.

A periodic tiling is a tiling that does not have two non-parallel shift symmetries. Simply put, a periodic tiling has two directions, when shifted towards which the entire pattern will be combined with itself.
This principle can be used for practical purposes. The tiling can be very difficult, but if you need to tile in the bathroom or parquet in the living room, it will be enough to use the same tiles in the shape of a parallelogram.
The problem of finding parquets with given properties has long attracted mathematicians. Thus, there are only three tilings of the plane by regular polygons of the same kind. Such parquets can be laid out from equilateral triangles, squares and regular hexagons. They are also called " Platonic parquets ".
There are more than eight parquets in which it is allowed to use several types of regular figures at the same time, and at the same time they retain a high degree of symmetry (any two vertices in them are connected by a symmetry transformation that transforms the parquet into itself). Such parquets are called archimedean .
You can periodically tile the plane with any triangle and any quadrilateral. There are also 15 pentagons that allow you to periodically tile the plane .
Mathematicians have long wanted to show non-periodic parquets. In the 60s, an example of such a parquet was invented by the Chinese mathematician Hao Wang, but to lay out his parquet, it would take 20,426 types of tiles: all of his tiles were square, but differed in the colors of the edges, while the parquet had to be assembled so that the adjacent edges were the same color. Then Wang's parquet was assembled from 11 types of multi-colored tiles.
The famous mathematician Roger Penrose managed to assemble a non-periodic parquet from two tiles .


